In this four-part series, the EdReports mathematics team explores the Standards for Mathematical Practice and why they’re essential for every student to learn and grow. Read the rest of the series here:
- How Math Practices 1–3 Help All Students Access Math Learning and Build Skills for the Future
- How Math Practices 5 and 6 Build Student Confidence and Ownership of Their Learning
- How Math Practices 7 and 8 Power Student “Lightbulb” Moments
Think back to your days in secondary school. Most of us learned mathematics as a straight line: starting at one place with a question and following a predetermined path to arrive at a final answer. But over time through my own learning and experience as an educator, I came to understand that in reality mathematics is nothing like this. Mathematics is all about creatively solving problems and exploring different possibilities.
In our series on the importance of the Standards for Mathematical Practice, we’ve examined the ways in which the Practices support students to build crucial mathematical and critical thinking skills while connecting students to math in the world around them. Math Practice Four: Model with Mathematics (MP4) is no exception, and in most instances, MP4 encompasses some or all of the other seven Math Practices.
Rather than a straight line, mathematical modeling is more like a never ending circle. Through real-world situations, students determine how to best solve the questions in front of them. For example: how much paint is needed to paint an entire house? How can a school stay within a budget of $6 per student and meet nutritional needs? Or, which baseball team out of the 30 major league teams is the best?
Asking questions like these not only makes mathematics relevant and exciting, but demands that students do more than consider one method for solving a single equation. The open-endedness of mathematical modeling also prompts students to use their individual and collective expertise. This inspires agency and belonging, within mathematics and across subject areas, in ways that can develop social and emotional competencies.
The practice of modeling makes students leaders in their own learning experience and challenges them to not simply make calculations but to also consider problems from various perspectives. As students encounter and negotiate those perspectives, they are able to connect knowledge from multiple disciplines and create new knowledge.
The practice of modeling makes students leaders in their own learning experience and challenges them to not simply make calculations but to also consider problems from various perspectives.
This focus on critical thinking, problem-solving, the value of multiple points of view, and developing mathematical skills is integral to preparing students for life beyond high school. It is why modeling is stressed in rigorous college and career-ready standards.
Mathematical Modeling Deep Dive
To better understand why mathematical modeling can be transformative for students, it’s important to see it in action. Let’s explore mathematical modeling with the baseball question I posed earlier: which is the best team?
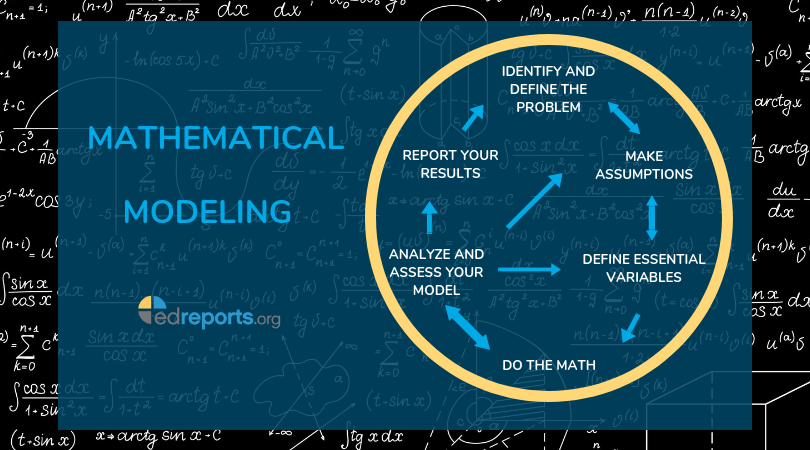
Determining the problem and making assumptions
The first step in modeling often involves focusing on and defining subjective words, and exploring the problem through research and brainstorming. To answer the question about which team is the best, students first need to determine what “best” means, and as they define ”best,” they need to consider the assumptions they are making in their definition.
For example: Does best mean the team with the most wins against teams of the same or better record? Does best mean the team with the most hits in clutch situations or go-ahead home runs in the seventh inning or later? Does best mean the team with the strongest pitching and defense? Or does it mean some combination of all these factors? If so, which qualities are we going to preference and by how much?
As students begin to define the problem and make assumptions, reducing the number of factors and simplifying the question will change the variables that make up the calculations and determine the conclusion they reach. Already, you can imagine that two different students could approach this same problem using different assumptions, leading to different mathematical content, and arrive at equally valid outcomes.
Defining variables, making calculations, analyzing and reporting your results
As students begin to determine which team is best, they can combine the variables they’ve defined with different calculations to arrive at their solutions. While certainly some kinds of questions will lend themselves to specific kinds of mathematics (i.e. algebra equations versus geometric models), the point of mathematical modeling is that students are able to exercise their own creativity, judgments, and knowledge of mathematics as they attempt to reach their conclusions.
What’s especially powerful about modeling is what happens after students get the answers they’re searching for. Then it’s time for them to share their findings and assess the strengths and weaknesses of their process, analyze whether or not the answer they arrived at makes sense, and consider how they might have done things differently.
This kind of examination and reflection is not as meaningful to students if there’s a fixed, final answer with a limited number of ways to get to the solution. With modeling, not only do students have to find a “best team” mathematically, they have to defend how they arrived at such a choice. Few learning opportunities test and stretch kids in so many different ways.
MP4 also provides opportunities for educators to affirm the cultural identities of their students and their students’ families by engaging in community-based problems that allow students to utilize their cultural and linguistic practices.
MP4 also provides opportunities for educators to affirm the cultural identities of their students and their students’ families by engaging in community-based problems that allow students to utilize their cultural and linguistic practices. I offered the example of baseball earlier, but questions could just as easily focus on students planning a picnic for their families and determining the supplies they’ll need, or exploring the impact of and solutions for environmental waste in a local community. The possibilities are endless for teachers to center student experiences in ways that support them to thrive.
Through mathematical modeling we can dispel the idea of mathematics as out of reach for most and only accessible to the lucky, talented few.
Through mathematical modeling we can dispel the idea of mathematics as out of reach for most and only accessible to the lucky, talented few. We have the chance to show students what mathematics can mean to their lives but, more than that, we can show them that they are in control of solving and creatively answering the questions they have always wondered about.
For example: Does best mean the team with the most wins against teams of the same or better record? Does best mean the team with the most hits in clutch situations or go-ahead home runs in the seventh inning or later? Does best mean the team with the strongest pitching and defense? Or does it mean some combination of all these factors? If so, which qualities are we going to preference and by how much?
As students begin to define the problem and make assumptions, reducing the number of factors and simplifying the question will change the variables that make up the calculations and determine the conclusion they reach. Already, you can imagine that two different students could approach this same problem using different assumptions, leading to different mathematical content, and arrive at equally valid outcomes.
The Role of Instructional Materials and How EdReports Reviews for the Math Practices
Through my work as a teacher and at EdReports, I’ve learned that one key way of ensuring that students have opportunities to participate in the math practices is through their materials. When teachers have access to high-quality curriculum, their instructional decisions are strengthened with problems and resources ready for classroom use.
The Math Practices and their meaningful connection to high-quality standards are central to the EdReports mathematics review tools. Our tools examine the ways in which materials support the intentional development of the Practices as integral to college and career-ready standards. As EdReports evaluates programs, we look for tasks that embrace the idea that there could be more than one answer, and that different assumptions and definitions could lead to different results. Mathematics becomes more than just numbers and variables in these materials: it’s about the possibility those numbers represent when combined with student ingenuity, creativity, logic, and analysis.
Instructional materials will not solve all the challenges in our mathematics classrooms, but they are integral to providing teachers with a foundation of resources that make it all the more likely that students will get to experience mathematics as full of possibility and with every door open.

